Sunday, January 20, 2013
What are properties of kites?
Kite
- Two pairs of consecutive congruent sides
- Diagonals are perpendicular
- The vertex diagonal Bisect the other diagonals
- The vertex diagonal is an angle bisector of the vertex angles
How can we prove that triangles are congruent?
Two Triangles- are congruent if and only if all their corresponding sides and angles are congruent.
 Side-Side-Side Triangle Postulate (SSS)- If 3 sides of a triangle are congruent to 3 sides of another triangle then the two triangles are congruent.
Side-Side-Side Triangle Postulate (SSS)- If 3 sides of a triangle are congruent to 3 sides of another triangle then the two triangles are congruent.
Triangles ABC=XYZ
Side-Angle-Side Triangle Postulate (SAS)- If 2 sides of a triangle and the included angle are congruent to the 2 sides of another triangle and its included angle ,
then the two triangles are congruent.Triangles ABC=XYZ
 Angle-Side-Angle (ASA)- triangles are congruent if any two angles and their included side are equal in both triangles.
Angle-Side-Angle (ASA)- triangles are congruent if any two angles and their included side are equal in both triangles.
Triangles ABC=XYZ

Angle-Angle-Side congruence Postulate (AAS)- Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangle.
Triangle ABC=XYZ
Triangles ABC=XYZ
Side-Angle-Side Triangle Postulate (SAS)- If 2 sides of a triangle and the included angle are congruent to the 2 sides of another triangle and its included angle ,
then the two triangles are congruent.Triangles ABC=XYZ
Triangles ABC=XYZ
Angle-Angle-Side congruence Postulate (AAS)- Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangle.
Triangle ABC=XYZ
How do we use the exterior angle thereom?
How do we use the triangle sum conjecture?
What are the special angles we can create with parallel lines?
Transverse- a line that intersects two or more other coplanar lines.
Corresponding angles- angles that are in the same position relative to the transverse and lines.<1=<5 ,<2=<6, <3=<7 ,<4=<8
Corresponding angles conjecture- if two parallel lines are cut by a transverse then corresponding angles are congruent.
<1=<5 ,<2=<6, <3=<7 ,<4=<8
Alternate interior angles conjecture-if two parallel lines are cut by a transverse ,then alternate interior angles are congruent.
<3=<6, <4=<5
Alternate exterior angles conjecture- they are congruent
<3=<6, <4=<5
Consecutive interior/exterior angles conjecture - they are supplementary <1=<8, <2=<7
What are the special segments of triangles?
What are the basic building blocks of geometry?
Point-a point specifies only location. It has no length ,width, or depth.We usually represent a point with a dot on paper and label it and make it have dimensions, while a true points dimension is 0.
Line-a line has only one dimension: length. It contains forever in two directions (so it has infinitive length), but it has no width at all. A line connects two points.

Line segment-a line that has two end points.
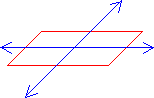
Plane-a plane is a flat, two dimensional object.

Ray-a line with one end point
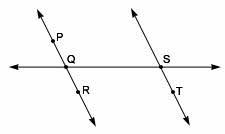
Collinear-a line on the same line
Coplanar-a plane on the same plane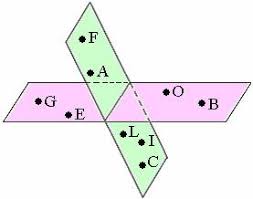
Line-a line has only one dimension: length. It contains forever in two directions (so it has infinitive length), but it has no width at all. A line connects two points.
Line segment-a line that has two end points.
Plane-a plane is a flat, two dimensional object.
Coplanar-a plane on the same plane
Friday, January 18, 2013
How to calculate the midpoint of a segment?
Subscribe to:
Comments (Atom)