25pi
Sunday, April 14, 2013
How do we calculate the surface area of a cylinder?
Thursday, March 28, 2013
How do we use conjuctions and disjunctions?
Conjuctions-Hooking up words and phrases and clauses with AND. A conjuction has two statements connected by and. A conjuction is true when both parts are true otherwise it is false.
Ex. Mary is on the softball team and Rob is on the football team.
Disjuctions-Hooking up words and phrases and clauses with OR. Two statements connected by or.A disjunction is false when both are false otherwise it is true.
Ex. Mary is on the softball team or Rob is on the football team.
Ex. Mary is on the softball team and Rob is on the football team.
Disjuctions-Hooking up words and phrases and clauses with OR. Two statements connected by or.A disjunction is false when both are false otherwise it is true.
Ex. Mary is on the softball team or Rob is on the football team.
Thursday, March 7, 2013
How Do We Do Compositions of Transformation?
Composition of Transformations-When two or more transformations are combined to form a new transformation , the result is called a composition of transformation
Example: (2,6)
Always do second transformation first
First reflect (2,6) over the x-axis.
x-axis (x,y)---(x,-y)
(2,6)---(2,-6)
Second dilation by multiplying by 2 in both x and y
2 multiplied by 2= 4 x=4
-6 multiplied by 2=-12 y=-12
(4,-12)
Final answer=(4,-12)
Example: (2,6)
Always do second transformation first
First reflect (2,6) over the x-axis.
x-axis (x,y)---(x,-y)
(2,6)---(2,-6)
Second dilation by multiplying by 2 in both x and y
2 multiplied by 2= 4 x=4
-6 multiplied by 2=-12 y=-12
(4,-12)
Final answer=(4,-12)
Sunday, January 20, 2013
What are the special Parallelograms?
What are properties of kites?
Kite
- Two pairs of consecutive congruent sides
- Diagonals are perpendicular
- The vertex diagonal Bisect the other diagonals
- The vertex diagonal is an angle bisector of the vertex angles
How can we prove that triangles are congruent?
Two Triangles- are congruent if and only if all their corresponding sides and angles are congruent.
 Side-Side-Side Triangle Postulate (SSS)- If 3 sides of a triangle are congruent to 3 sides of another triangle then the two triangles are congruent.
Side-Side-Side Triangle Postulate (SSS)- If 3 sides of a triangle are congruent to 3 sides of another triangle then the two triangles are congruent.
Triangles ABC=XYZ
Side-Angle-Side Triangle Postulate (SAS)- If 2 sides of a triangle and the included angle are congruent to the 2 sides of another triangle and its included angle ,
then the two triangles are congruent.Triangles ABC=XYZ
 Angle-Side-Angle (ASA)- triangles are congruent if any two angles and their included side are equal in both triangles.
Angle-Side-Angle (ASA)- triangles are congruent if any two angles and their included side are equal in both triangles.
Triangles ABC=XYZ

Angle-Angle-Side congruence Postulate (AAS)- Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangle.
Triangle ABC=XYZ
Triangles ABC=XYZ
Side-Angle-Side Triangle Postulate (SAS)- If 2 sides of a triangle and the included angle are congruent to the 2 sides of another triangle and its included angle ,
then the two triangles are congruent.Triangles ABC=XYZ
Triangles ABC=XYZ
Angle-Angle-Side congruence Postulate (AAS)- Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangle.
Triangle ABC=XYZ
How do we use the exterior angle thereom?
How do we use the triangle sum conjecture?
What are the special angles we can create with parallel lines?
Transverse- a line that intersects two or more other coplanar lines.
Corresponding angles- angles that are in the same position relative to the transverse and lines.<1=<5 ,<2=<6, <3=<7 ,<4=<8
Corresponding angles conjecture- if two parallel lines are cut by a transverse then corresponding angles are congruent.
<1=<5 ,<2=<6, <3=<7 ,<4=<8
Alternate interior angles conjecture-if two parallel lines are cut by a transverse ,then alternate interior angles are congruent.
<3=<6, <4=<5
Alternate exterior angles conjecture- they are congruent
<3=<6, <4=<5
Consecutive interior/exterior angles conjecture - they are supplementary <1=<8, <2=<7
What are the special segments of triangles?
What are the basic building blocks of geometry?
Point-a point specifies only location. It has no length ,width, or depth.We usually represent a point with a dot on paper and label it and make it have dimensions, while a true points dimension is 0.
Line-a line has only one dimension: length. It contains forever in two directions (so it has infinitive length), but it has no width at all. A line connects two points.

Line segment-a line that has two end points.
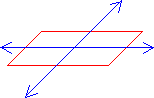
Plane-a plane is a flat, two dimensional object.

Ray-a line with one end point
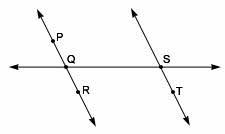
Collinear-a line on the same line
Coplanar-a plane on the same plane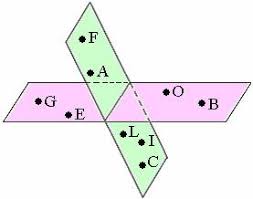
Line-a line has only one dimension: length. It contains forever in two directions (so it has infinitive length), but it has no width at all. A line connects two points.
Line segment-a line that has two end points.
Plane-a plane is a flat, two dimensional object.
Coplanar-a plane on the same plane
Friday, January 18, 2013
How to calculate the midpoint of a segment?
Subscribe to:
Comments (Atom)
